SpheriCo.jl

Summary: A Julia package for the Spherical Collapse of a scalar field in classical and semiclassical gravity.

Keywords: Julia, Numerical Simulations, Black Holes

Date: 24 March 2025

Introduction

The collapse of a scalar field with spherical symmetry in classical gravity (general relativity) has reached a good level of maturity and has unraveled the exciting phenomenon of critical collapse, that is the threshold between black hole formation and dispersion of the initial data. We call the former scenario supercritical and an apparent horizon (AH) forms and the latter subcritical (no AH). Near criticality we observe unique features such as self similarity of the solution and an echoing behaviour of the collapsing scalar field.

Understanding the same system when the classical scalar is promoted to a quantum field (semiclassical setup) is yet to be fully understood. In this semiclassical system we retain a classical geometry, but its dynamics are sourced by the expectation value of the quantum stress-energy tensor. To approximate this tensor we need to evolve as many quantum modes as possible, which is computationally expensive. Restricting to spherical symmetry makes the problem more managable, but one still needs to evolve a large number of modes to capture the quantum effects and also resolve coordinate singularities near the origin of the radial domain. Overcoming these challenges however can have a great payoff, since we can examine behavior that is not present in the classical system, such as looking for Hawking radiation and correlations in the scalar field between points that are separated across the horizon, which are interpreted as correlations between pairs of Hawking quanta. SpheriCo.jl has improved our previous abilities to perform such simulations, and has already been used to study quantum correlators across the black hole apparent horizon.

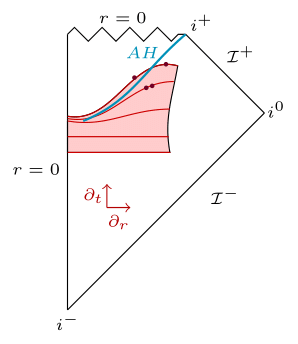
Hawking quanta inside and outside the black hole apparent horizon

Hawking quanta (red dots) inside and outside the black hole apparent horizon (AH)

Main results

A challenge present in many studies of gravitational collapse is the approximation of the evolved variables near r = 0, since terms of the form 1/r appear in their equations of motion. This challenge becomes increasingly difficult in the semiclassical setup, where these terms can become very large and render the equations stiff. This seems to have been the main reason for driving earlier semiclassical simulations on the topic only stable for a short time. By combining the summation-by-parts operators of Gundalch, Martin-Garcia, and Garfinkle with the convenient evolved variables of Alcubierre and Gonzalez, together with Banjamin Berczi, Magdalena Eriksson, and Paul Saffin, we manage to perform semiclassical simulations for longer than it was previously possible, and explore quantum correlations of events across an apparent horizon.

In Quantum correlations in a gravitational collapse simulation with SpheriCo.jl we present an extensive suit of tests for the code that assess its accuracy and stability, both for the classical and quantum fields. We are able to observe critical behavior of gravitational collapse for the classical setup, in agreement with expected results. This is a non-trivial result, especially given that to our knowledge the specific summation-by-parts operators have not been used again in this case, and are originally constructed for a different setup. We also compute the two-point correlation functions, with results that hint at a non-trivial correlation across the horizon of Hawking quanta. Videos with the evolution of the quantum correlators are available here.

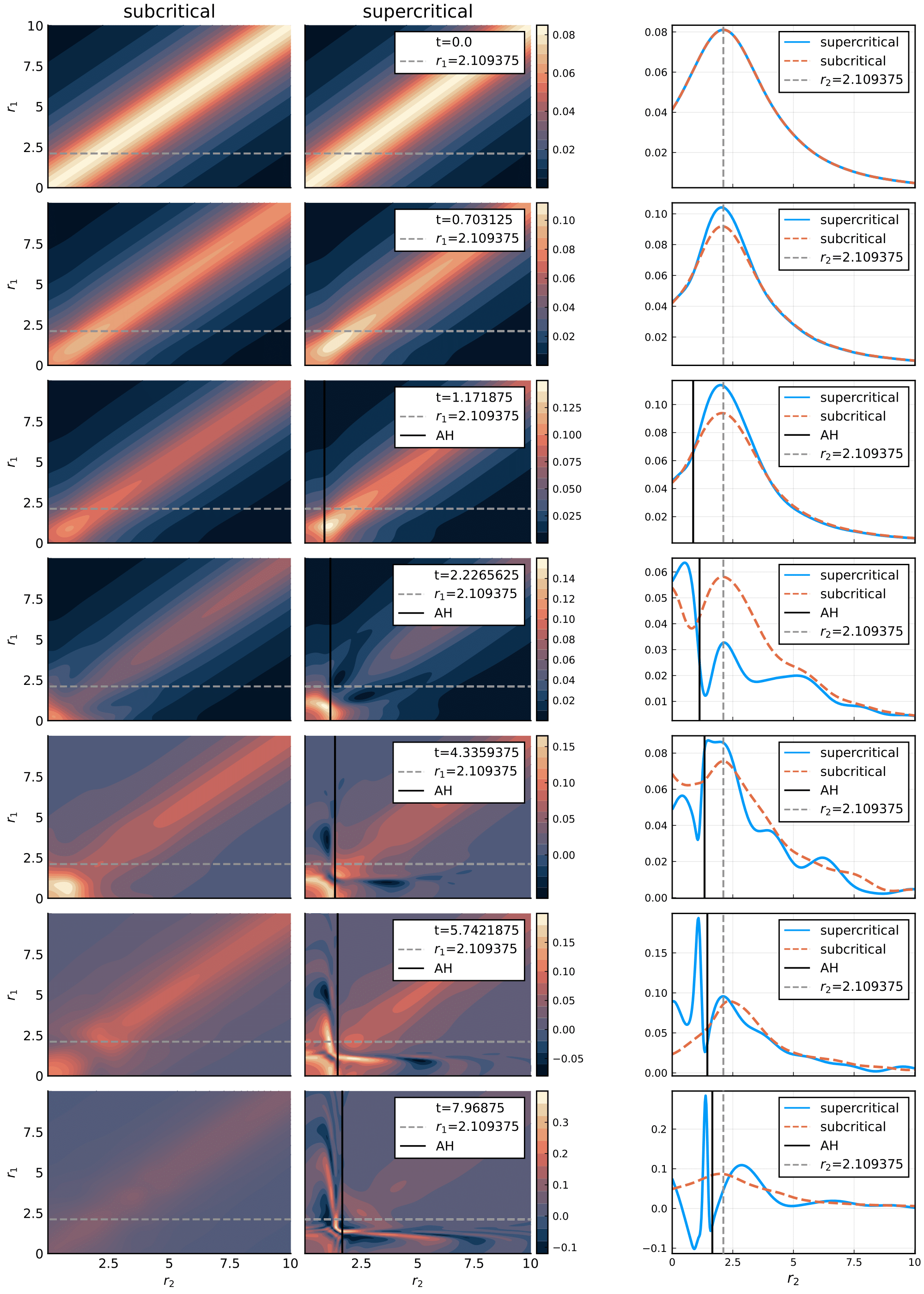
Quantum correlators across the black hole apparent horizon

Quantum correlators for a subcritical (no AH) and supercritical (AH exists) simulations

Future Work

There are various different avenues one can take to further develop this project and improve SpheriCo.jl. For instance, a possible direction is to work on the mathematical formulation of the equations solved, such that the constraint violation is improved and a dynamical shift is included in the metric ansatz. The latter can allow us to have stable near-critical simulations for the semiclassical setup, and more economic simulations for the classical one, since we could then increase the resolution near the origin without numerical regridding. Another idea is to add the possibility of finite difference summation-by-parts operators of higher order, which could then improve the accuracy of the simulations, making it especially important for the approximation of the quantum fields and their backreaction on the classical geometry. Experimenting with different lapse conditions can also be benificial in understanding the shape of the quantum correlators across the apparent horizon in different foliations.