Convergence tests in a lopsided normAbstract
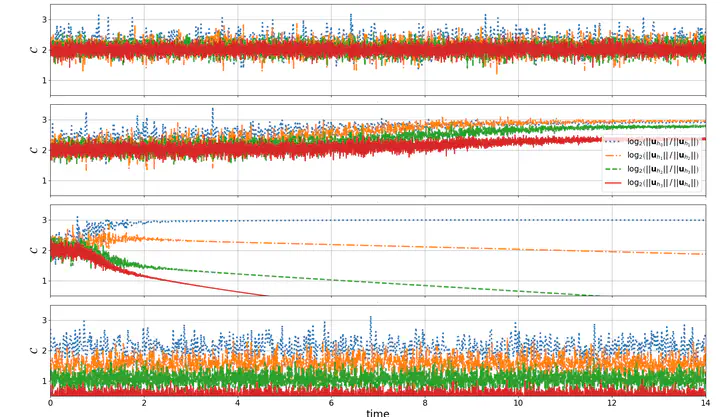
Bondi-like (single-null) characteristic formulations of general relativity are used for numerical work in both asymptotically flat and anti–de Sitter spacetimes. The well posedness of the resulting systems of partial differential equations, however, remains an open question. The answer to this question affects accuracy and, potentially, the reliability of conclusions drawn from numerical studies based on such formulations. A numerical approximation can converge to the continuum limit only for well-posed systems; for the initial value problem in the L2 norm, this is characterized by strong hyperbolicity. We find that, due to a shared pathological structure, the systems arising from the aforementioned formulations are, however, only weakly hyperbolic. We present numerical tests for toy models that demonstrate the consequence of this shortcoming in practice for the characteristic initial boundary value problem. Working with alternative norms in which our model problems may be well posed, we show that convergence may be recovered. Finally, we examine the well posedness of a model for Cauchy-characteristic matching in which model symmetric and weakly hyperbolic systems communicate through an interface, with the latter playing the role of general relativity in the Bondi gauge on characteristic slices. We find that, due to the incompatibility of the norms associated with the two systems, the composite problem does not naturally admit energy estimates.
Thanasis Giannakopoulos
Research Fellow
Researcher working on gravitational physics and scientific computing.